Características de las funciones exponenciales. Las funciones exponenciales tienen las siguientes propiedades: El dominio de una función exponencial son todos los números reales, o dicho con otras palabras, una función exponencial existe por cualquier valor de x.. Encuentra una función exponencial que pase por los puntos ( − 2, 6) y (2, 1). Solución. Debido a que no tenemos el valor inicial, sustituimos ambos puntos en una ecuación de la forma f(x) = abx, y luego resolvemos el sistema para a y b. Sustitución ( − 2, 6) da 6 = ab − 2. Sustitución (2,1) da 1=ab^2.

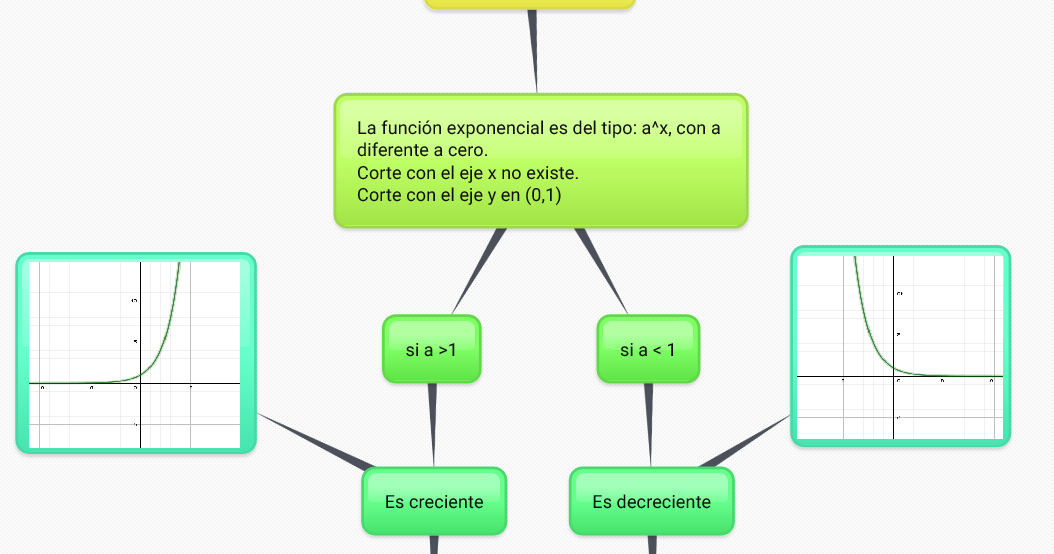
Función Exponencial

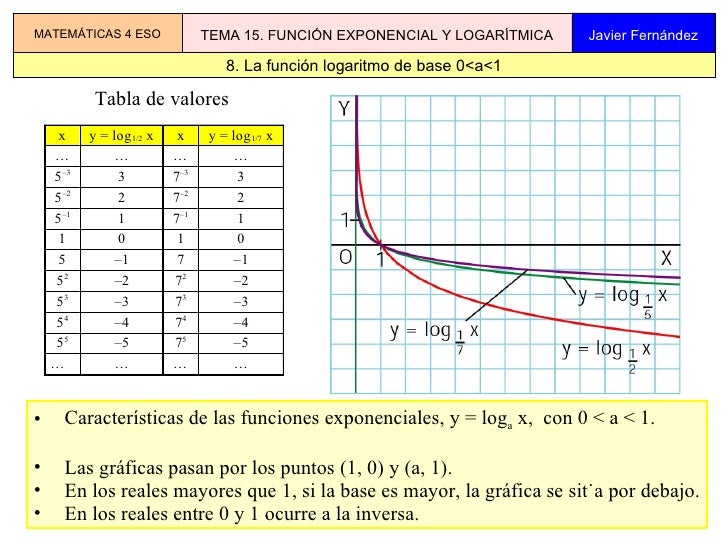
Tema 15 Funciones Exponenciales Y Logaritmicas

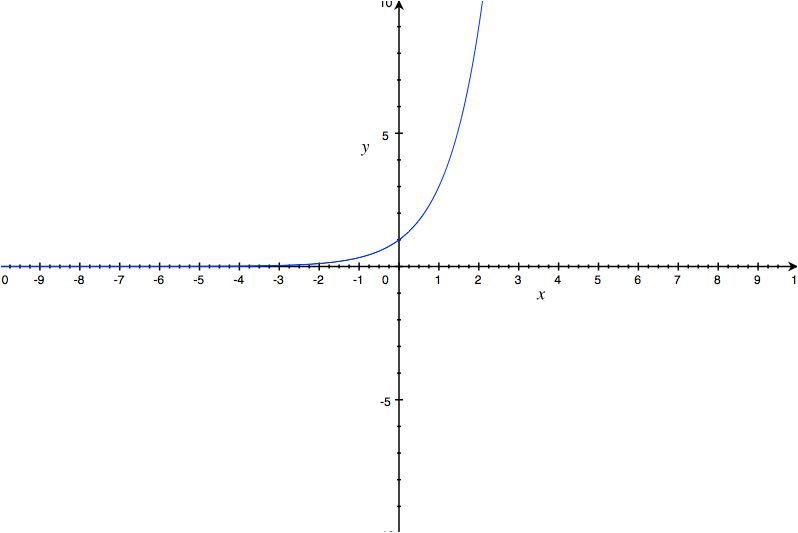
Función exponencial Aulaprende

Función Exponencial Características YouTube

Funciones Exponenciales D La funcin exponencial con base

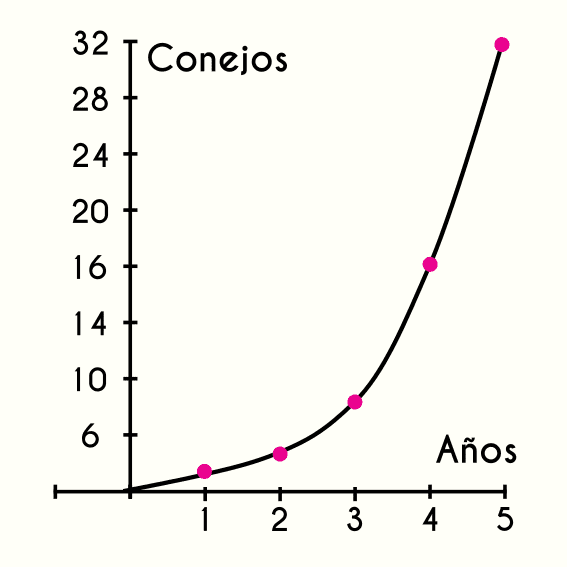
EJEMPLOS de Función exponencial con Definición Fhybea

Función Exponencial YouTube

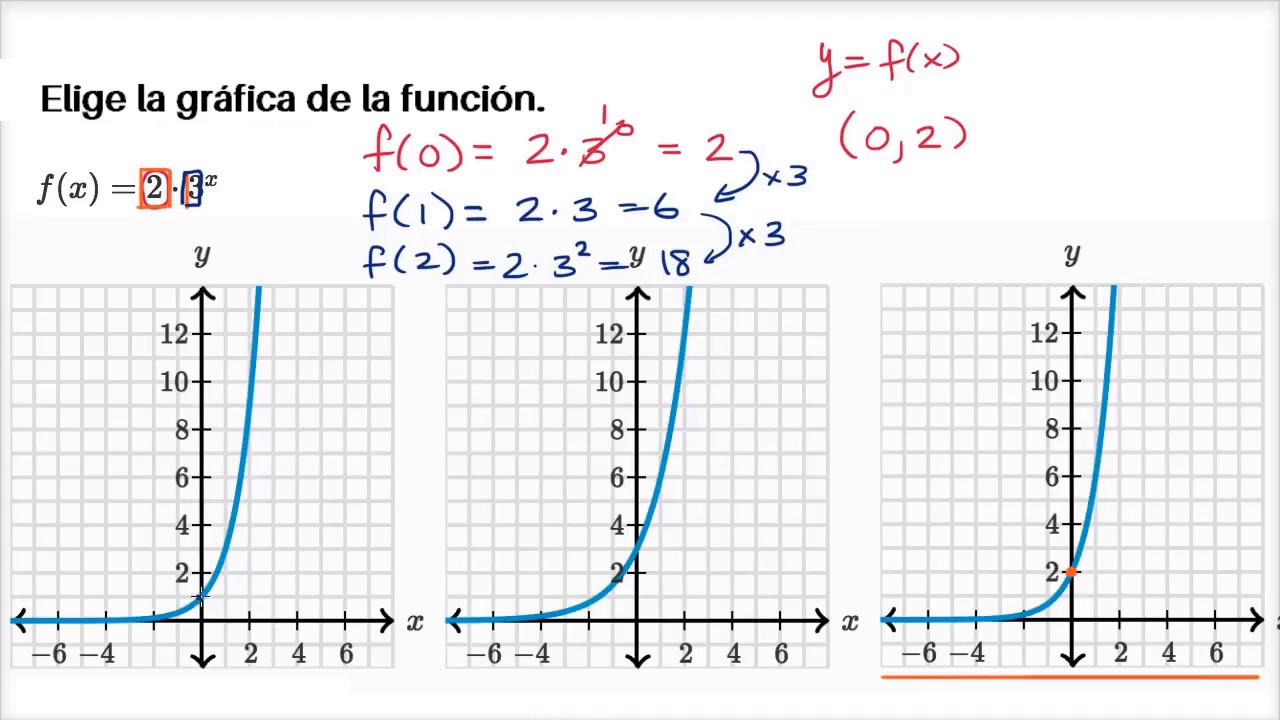
Identificar la gráfica de una función exponencial Khan Academy en Español YouTube

Cómo graficar una función exponencial YouTube

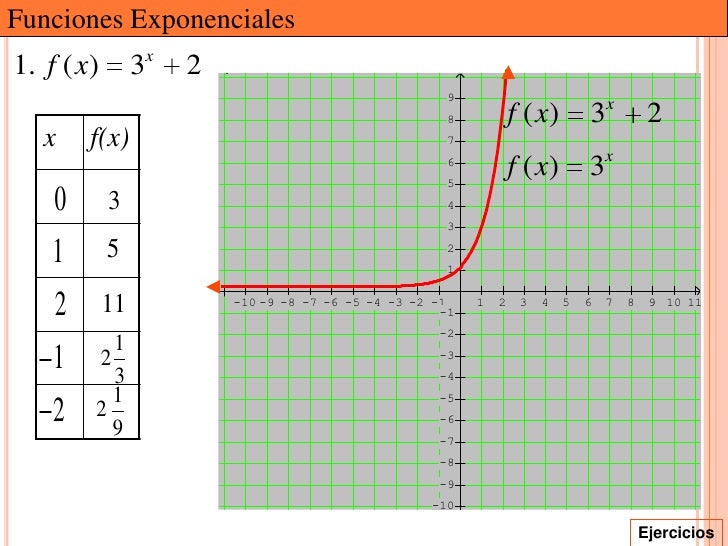
Forma General Y Modelo Grafico De La Funcion Exponencial Formă Blog

Función Exponencial YouTube

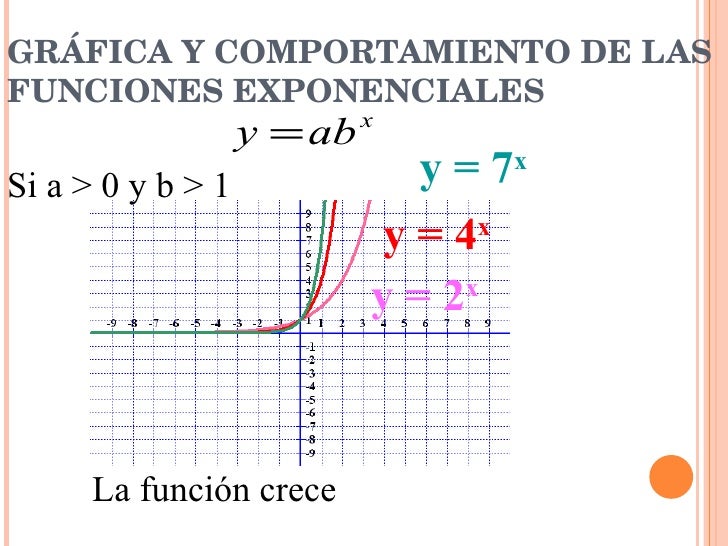
Funciones Exponenciales

Función exponencial características YouTube

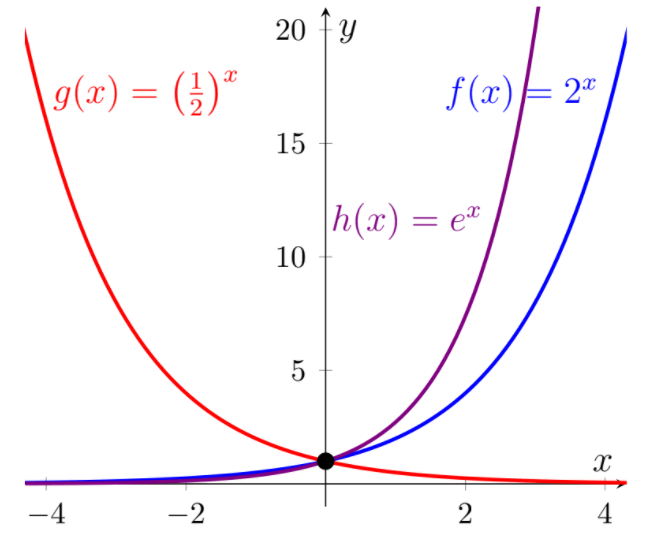
Significado de función exponencial «Definición, ejemplos, gráfica creciente y decreciente»

Función exponencial YouTube

Gráficas de Funciones Exponenciales Neurochispas

Funciones EXPONENCIALES 💹 Y Función EXPONENCIAL NATURAL [e] (Gráficas, Propiedades y Forma

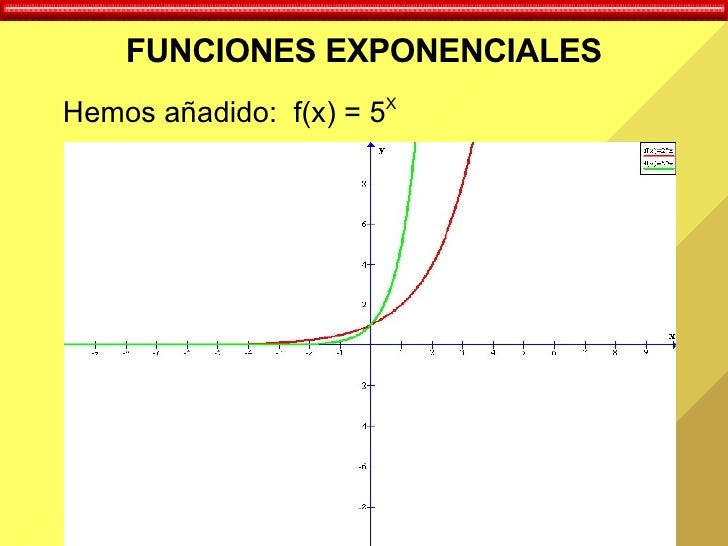
FUNCIONES EXPONENCIALES

Funciones Exponenciales La función exponencial con base a se define para todos los números

Gráficas de Funciones Exponenciales Neurochispas

La función exponencial natural y = e x. En matemáticas, una función exponencial es una función de la forma en el que el argumento x se presenta como un exponente. Una función de la forma también es una función exponencial, ya que puede reescribirse como: Como funciones de una variable real, las funciones exponenciales se caracterizan.. Este tema cubre: - Radicales y exponentes racionales - Gráficas y comportamiento en los extremos de funciones exponenciales - Manipulación de expresiones exponenciales al usar propiedades de exponentes - Crecimiento y decaimiento exponencial - Modelar con funciones exponenciales - Resolver ecuaciones exponenciales - Propiedades de logaritmos Resolver ecuaciones logarítmicas - Graficar.