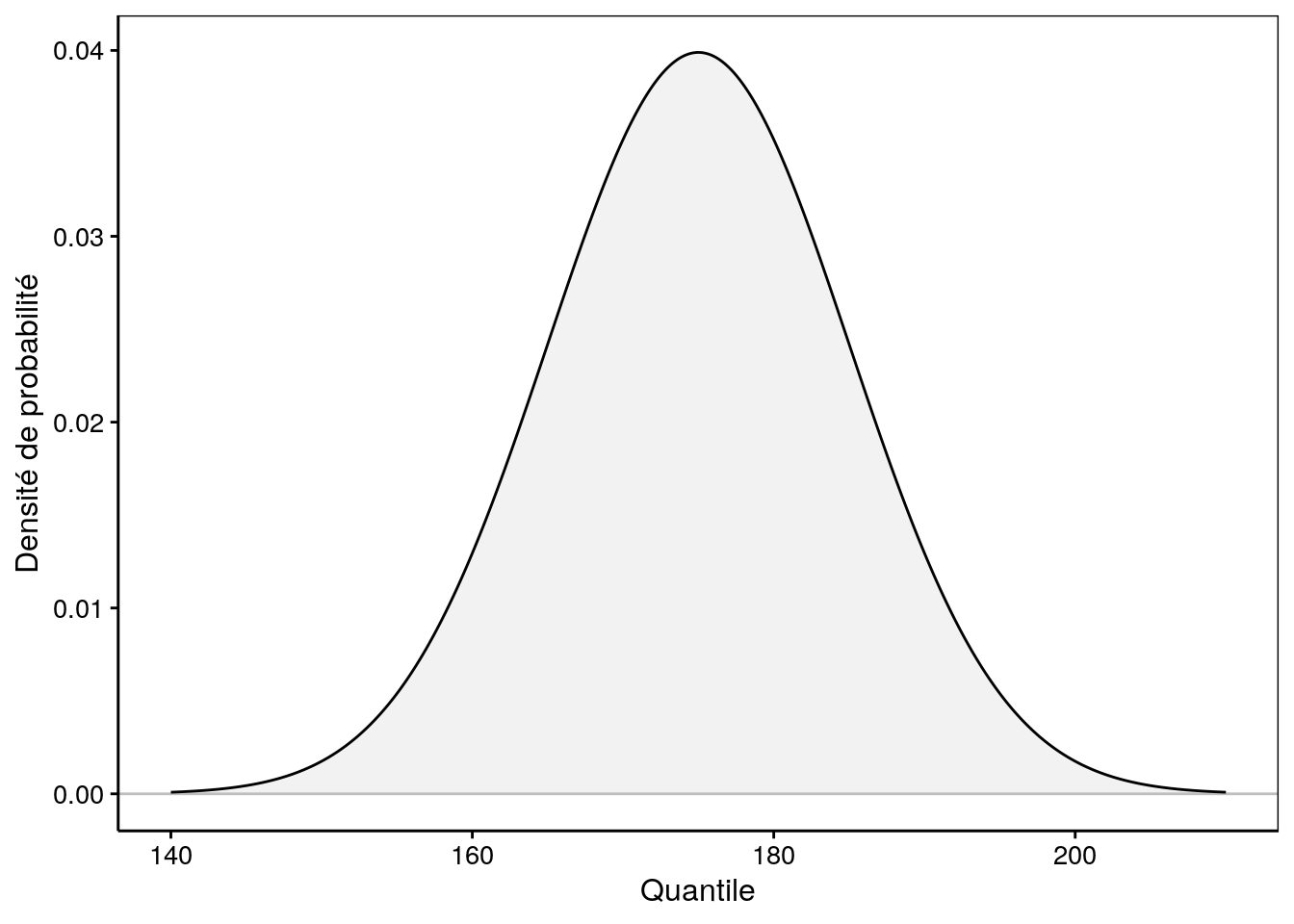
Normal Distribution Overview. The normal distribution, sometimes called the Gaussian distribution, is a two-parameter family of curves. The usual justification for using the normal distribution for modeling is the Central Limit theorem, which states (roughly) that the sum of independent samples from any distribution with finite mean and variance converges to the normal distribution as the.. chapitre 5: La loi normale. 1. Loi normale ou de Gauss. Supposons que nous tirions des échantillons aléatoires d'une population dont la taille moyenne est de 170 cm , avec un écart type de 10 cm . Traçons l'histogramme de la taille, avec des classes de 5 cm de large, pour des échantillons de plus en plus grands.

Loi normale et courbe de Gauss GeoGebra
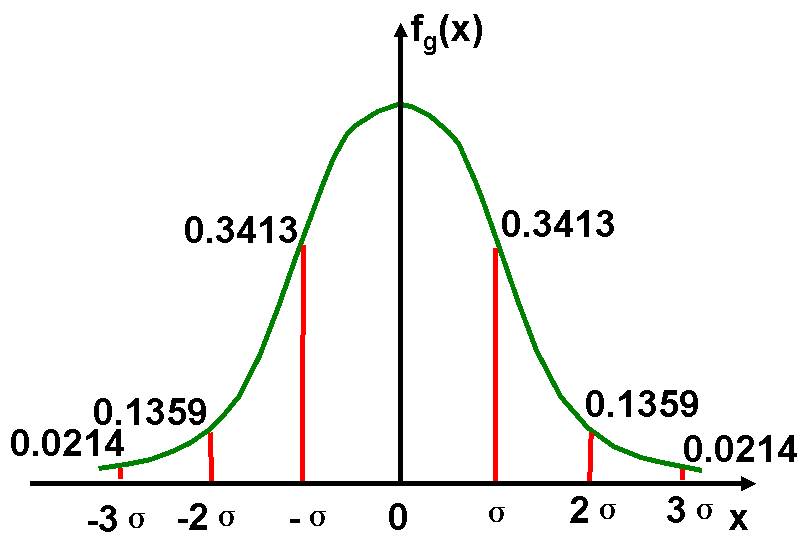
Gaussian Distribution

Diagramme De Distribution Normale Ou Courbe Gaussienne De Bell Sur Le Tableau Illustration de
Gauss distribution. Standard normal distribution. Gaussian bell graph curve. Business and

COURS N°5 Loi Normale 1ère Partie Abamaths
3 La Courbe de Gauss (source htt ps // f Download Scientific
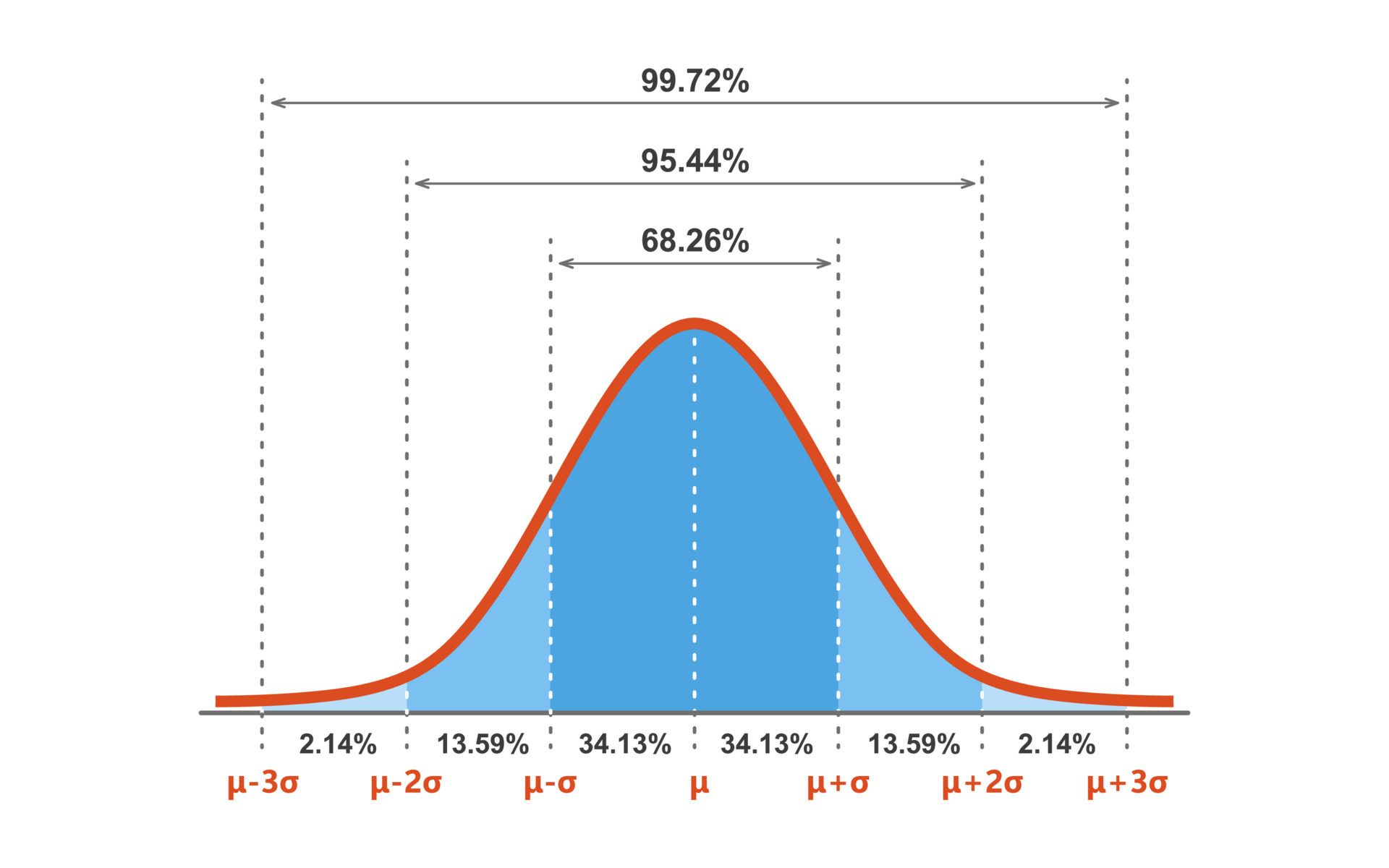
Gauss distribution. Standard normal distribution. Gaussian bell graph curve. Business and
Gauss distribution. Standard normal distribution. Gaussian bell graph curve. Business and
7.6 Distribution Normale Science des données biologiques I
Gaussian distribution Banque de photographies et d’images à haute résolution Alamy
La Loi normale, loi de Gauss
Gauss distribution. Standard normal distribution. Gaussian bell graph curve. Business and
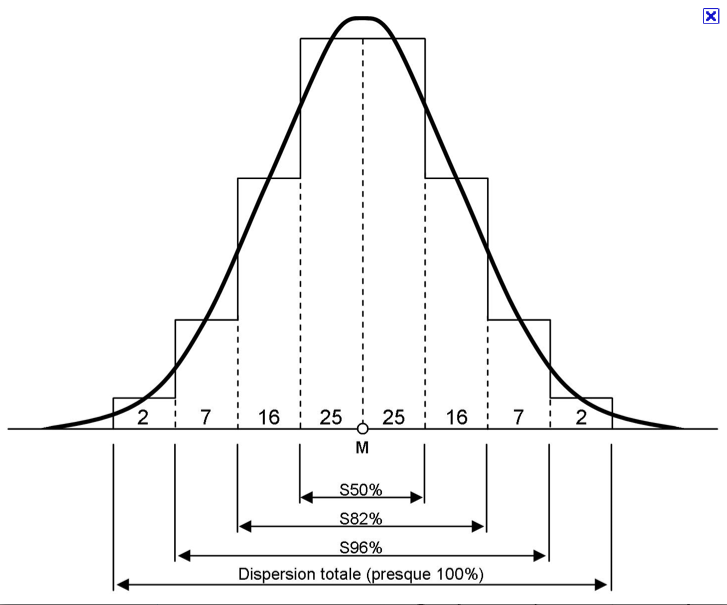
courbe de Gauss

Gaussien, Cloche Ou Courbe De Distribution Normale Image stock Image du progrès, distribution

Diagramme De Distribution Normale Ou Courbe Gaussienne De Bell Sur Le Tableau Illustration de
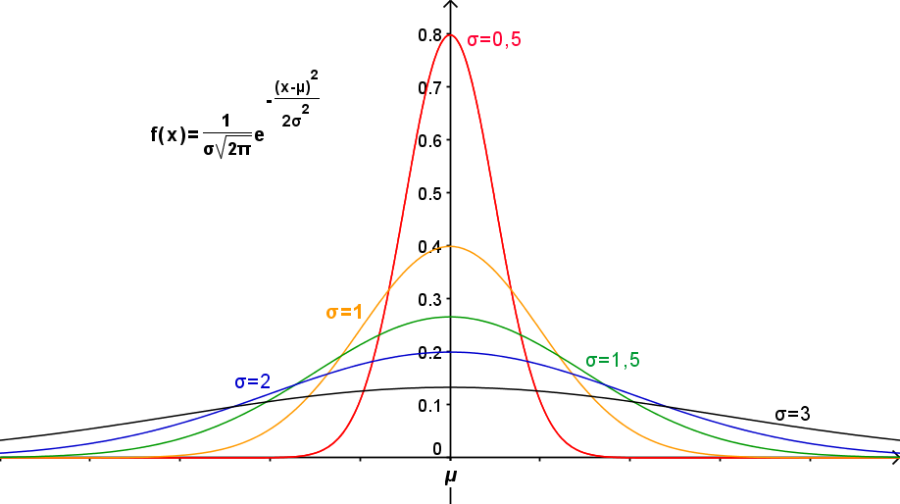
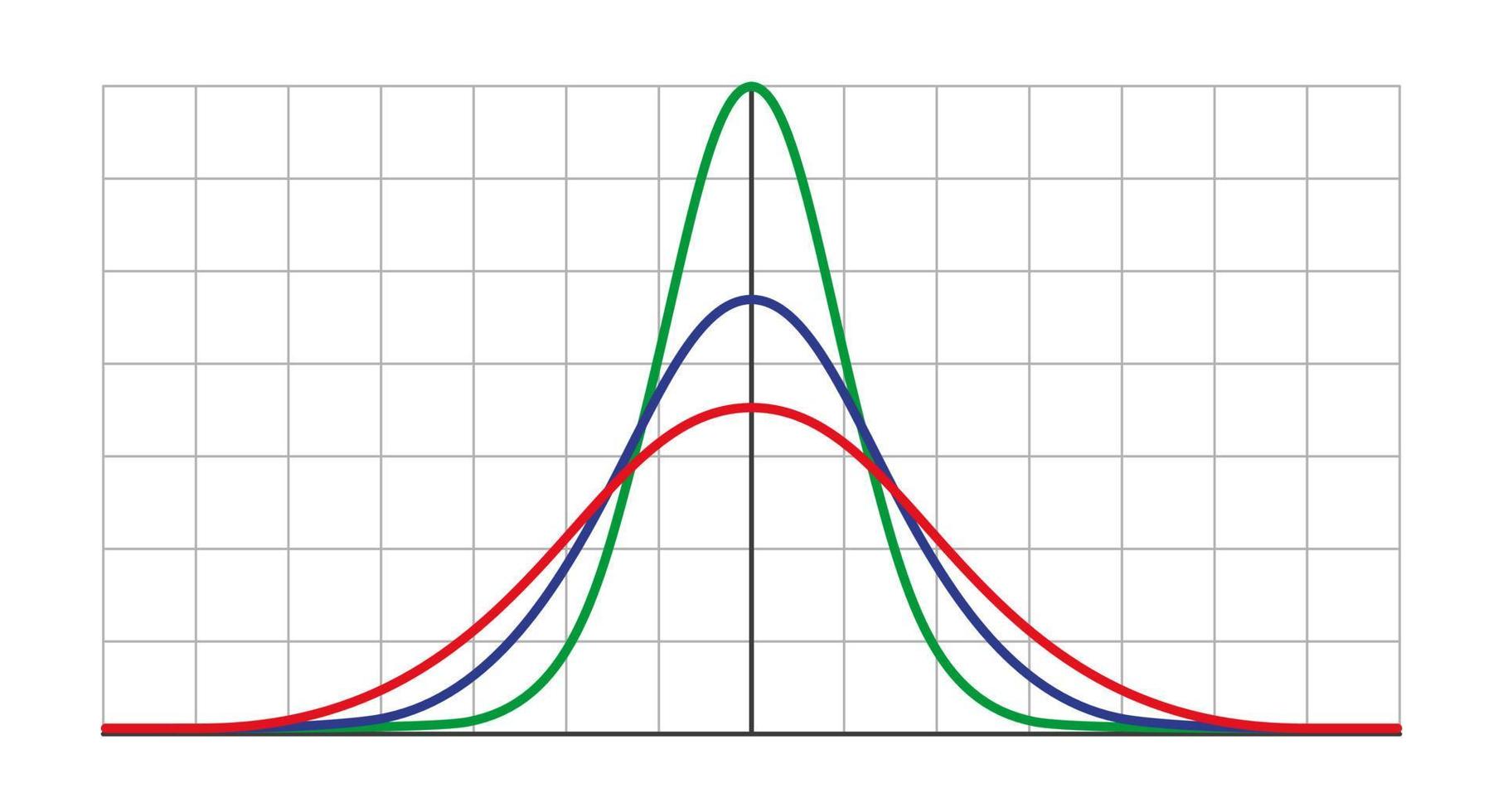
Figure 20 Courbes de Gauss en fonction de σ (même moyenne)

Courbe gaussienne définition et importance en data science
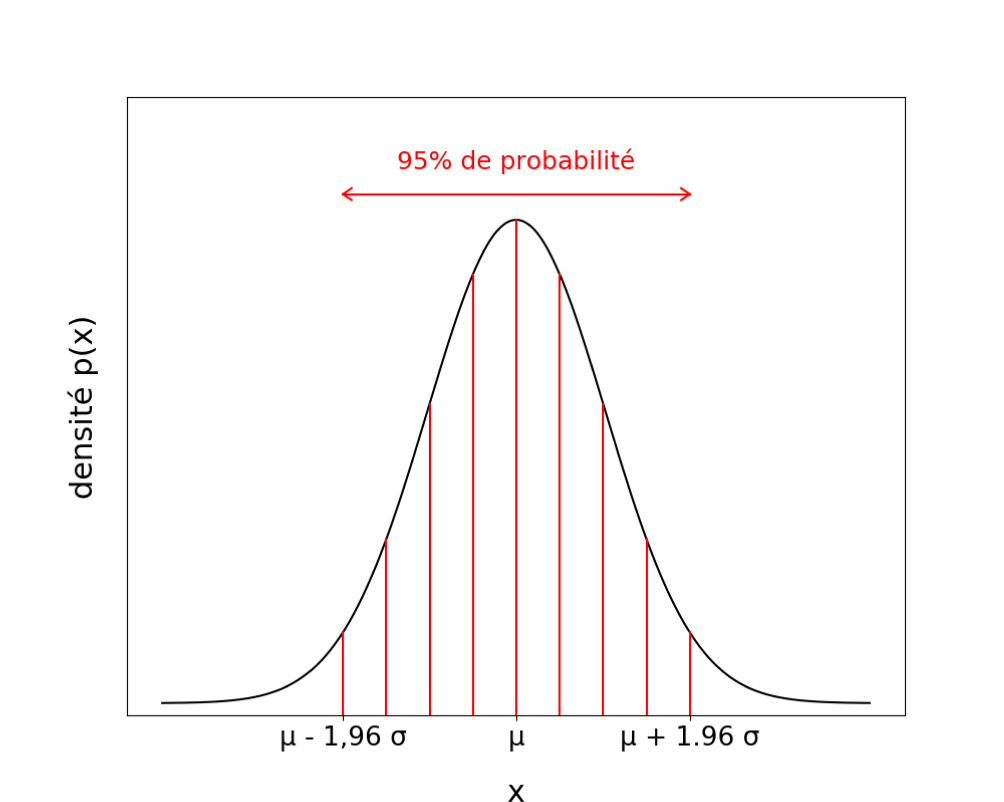
Loi gaussienne Data Analytics Post

Distribution De Gauss Distribution Normale Standard Courbe Graphique En Cloche Gaussienne
Distribution normale, aussi distribution gaussienne ou courbe en cloche. Très commun dans la
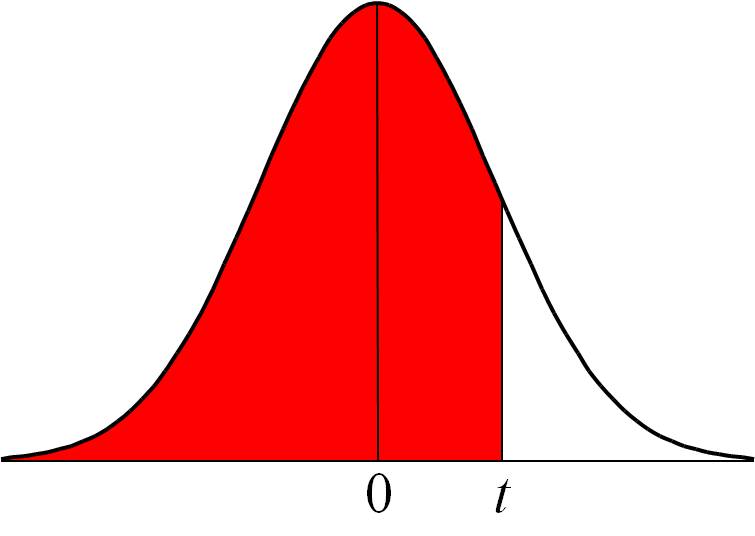
Planche de Galton. à la Cité de Sciences de La Vilette Paris. La courbe de Gauss apparaît comme densité de probabilité (les probabilités d'observations dans un intervalles sont calculées à l'aide d'une intégrale sur cet intervalle).. La représentation graphique de cette densité est une courbe en cloche (ou courbe de Gauss). Moments. Les moments de cette loi existent tous. Pour tout , le moment d'ordre n par rapport à l'origine est :. Pour la suite on supposera μ = 0 et σ 2 = 1. En raison de la parité de l' intégrande, tous les moments d'ordre impair sont nuls :